【FP3級の勉強02】資金計画で使う6つの係数

こんにちは
当ブログをご覧いただきありがとうございます。

今回は、FPの勉強で始めにつまずく難関である6つの係数の勉強です！！

先に結論から。
これを読んで難しいと思ったらここは捨ててください！！！
試験に受かるためには１問くらい捨てても全く問題ありません。
それでは以下ご覧ください。

資金計画を立てるときに将来価値※1や現在価値※2を計算する必要がありますが、その時にこの6つの係数を使用することで必要な資金の計算がラクにできるようになります。

※1　現在所有している金額に対して将来のある時点での価値に計算し直した金額のこと
※2　将来受け取れる金額を現時点の価値で計算し直した金額のこと

６つの係数

①終価係数　[しゅうか]
②現価係数　[げんか]
③年金終価係数　[ねんきんしゅうか]
④減債基金係数　[げんさいききん]
⑤年金現価係数　[ねんきんげんか]
⑥資本回収係数　[しほんかいしゅう]
があります。

終価係数

終価係数とは？

終価係数は、今持っているお金が将来どれだけ増えるかを計算するための数字です。

具体的にどういうこと？

例えば、100円を貯金して、1年後にどれだけ増えるかを知りたいとします。このとき、銀行が「毎年5%の利子をつけます」と言っているとしましょう。

今のお金：100円
利子：5%（0.05）

100円 × 終価係数 = 1年後のお金

1年後の終価係数は1.05です。つまり、

100円 × 1.05 = 105円

1年後に105円になります。

もう少し詳しく

2年後のお金を知りたい場合は、次のようにします。

1年後の105円 × 終価係数 = 2年後のお金 105円 × 1.05 = 110.25円

このように、毎年の終価係数を使ってお金がどれだけ増えるかを計算します。

終価係数のまとめ

終価係数は、お金が時間とともにどれだけ増えるかを示す数字です。お金を銀行に預けて利子がつくときに、終価係数を使って将来のお金の額を計算します。例えば、100円を預けると、1年後には105円、2年後には110.25円になるということです。

現価係数

現価係数とは？

現価係数は、将来のお金が今どれくらいの価値があるかを計算するための数字です。

具体的にどういうこと？

例えば、将来100円をもらえるとしたら、その100円が今の価値でどれくらいになるかを知りたいとします。このとき、銀行が「毎年5%の利子をつけます」と言っているとしましょう。

将来のお金：100円
利子：5%（0.05）

100円 × 現価係数 = 今の価値

1年後の現価係数は1 ÷ 1.05 ≈ 0.952です。つまり、

100円 × 0.952 ≈ 95.2円

1年後に100円もらえるとしたら、それは今の価値で約95.2円になります。

もう少し詳しく

2年後に100円もらえる場合を考えます。この場合、2年後の現価係数は次のように計算します。

現価係数 = 1 ÷ (1.05 × 1.05) ≈ 0.907

100円 × 0.907 ≈ 90.7円

2年後に100円もらえるとしたら、それは今の価値で約90.7円になります。

現価係数のまとめ

現価係数は、将来のお金が今どれくらいの価値があるかを示す数字です。将来もらうお金の価値を今の価値に換算するときに使います。例えば、1年後に100円もらえるとしたら、それは今の価値で約95.2円、2年後に100円もらえるとしたら今の価値で約90.7円になるということです。

年金終価係数

年金終価係数とは？

年金終価係数は、毎年少しずつ貯めたお金が、将来どれだけ増えるかを計算するための数字です。たとえば、お年玉を毎年貯金して、それが将来どれだけになるかを知るために使います。

具体的にどういうこと？

例えば、毎年100円ずつ貯金するとします。銀行が「毎年5%の利子をつけます」と言っているとしましょう。

毎年の貯金：100円
利子：5%（0.05）
貯金の期間：3年間

毎年貯めたお金がどれだけ増えるかを計算します。

計算の方法

まず、年金終価係数を求めるために、以下の式を使います

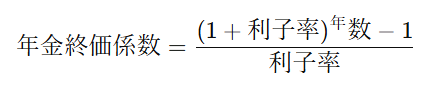
利子率が5%（0.05）、貯金の期間が3年間の場合、計算は次のようになります

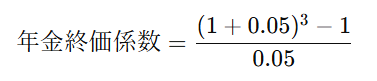
計算をすると

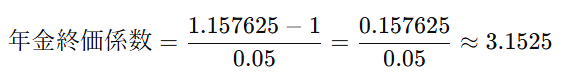
具体例

毎年100円ずつ3年間貯金すると、その貯金の合計額は次のようになります：毎年の貯金額×年金終価係数=100円×3.1525≈315.25円毎年の貯金額 × 年金終価係数 = 100円 × 3.1525 ≈ 315.25円毎年の貯金額×年金終価係数=100円×3.1525≈315.25円

つまり、毎年100円ずつ3年間貯金すると、3年後には315.25円になります。

年金終価係数のまとめ

年金終価係数は、毎年少しずつ貯めたお金が、将来どれだけ増えるかを計算するための数字です。たとえば、毎年100円を貯金すると、3年後にはそれが315.25円になるということです。この係数を使うことで、将来の貯金額を簡単に計算できます。

減債基金係数

減債基金係数とは？

減債基金係数は、将来のある金額を貯めるために、毎年いくらずつ貯金すればいいかを計算するための数字です。たとえば、5年後に1000円を貯めるためには、毎年いくら貯金すればよいかを知るために使います。

具体的にどういうこと？

例えば、5年後に1000円を貯めたいとします。銀行が「毎年5%の利子をつけます」と言っているとしましょう。

目標の金額：1000円
利子：5%（0.05）
貯金の期間：5年間

このとき、毎年いくら貯金すればよいかを減債基金係数を使って計算します。

計算の方法

まず、減債基金係数を求めるために、以下の式を使います

利子率が5%（0.05）、貯金の期間が5年間の場合、計算は次のようになります

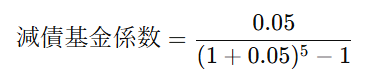
計算をすると

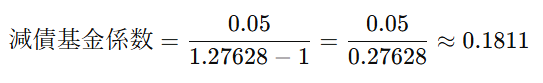
具体例

5年後に1000円を貯めるためには、毎年いくら貯金すればいいかを計算します：毎年の貯金額=目標の金額×減債基金係数=1000円×0.1811≈181.1円毎年の貯金額 = 目標の金額 × 減債基金係数 = 1000円 × 0.1811 ≈ 181.1円毎年の貯金額=目標の金額×減債基金係数=1000円×0.1811≈181.1円

つまり、5年後に1000円を貯めるためには、毎年約181.1円ずつ貯金すればよいということです。

減債基金係数のまとめ

減債基金係数は、将来のある金額を貯めるために、毎年いくらずつ貯金すればいいかを計算するための数字です。たとえば、5年後に1000円を貯めるためには、毎年約181.1円ずつ貯金すればよいということです。この係数を使うことで、目標金額に達するための毎年の貯金額を簡単に計算できます。

年金現価係数

年金現価係数とは？

年金現価係数は、将来にわたって毎年もらえるお金が、今どれくらいの価値があるかを計算するための数字です。たとえば、お小遣いを毎年もらえるとして、それが今の価値でどれくらいになるかを知るために使います。

具体的にどういうこと？

例えば、毎年100円を5年間もらえるとします。銀行が「毎年5%の利子をつけます」と言っているとしましょう。

毎年もらうお金：100円
利子：5%（0.05）
期間：5年間

このとき、これらのお金が今の価値でどれくらいになるかを年金現価係数を使って計算します。

計算の方法

まず、年金現価係数を求めるために、以下の式を使います

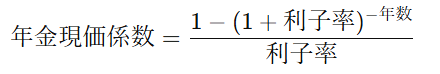
利子率が5%（0.05）、期間が5年間の場合、計算は次のようになります

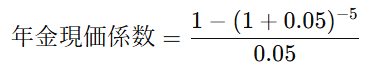
計算をすると

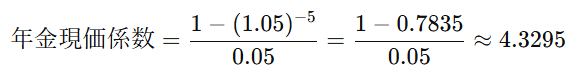
具体例

毎年100円を5年間もらう場合、それが今の価値でどれくらいになるかを計算します

つまり、毎年100円を5年間もらえると、それは今の価値で約432.95円になります。

年金現価係数のまとめ

年金現価係数は、将来にわたって毎年もらえるお金が、今どれくらいの価値があるかを示す数字です。たとえば、毎年100円を5年間もらえると、それは今の価値で約432.95円になるということです。この係数を使うことで、将来の定期的なお金の価値を今の価値に換算できます。

資本回収係数

資本回収係数とは？

資本回収係数は、将来にわたって毎年一定の金額をもらうためには、今どれくらいのお金を投資すればいいかを計算するための数字です。たとえば、将来毎年のお小遣いをもらうために、今どれだけ貯金しておけばいいかを知るために使います。

具体的にどういうこと？

例えば、将来毎年100円ずつ5年間もらいたいとします。銀行が「毎年5%の利子をつけます」と言っているとしましょう。

毎年もらいたいお金：100円
利子：5%（0.05）
期間：5年間

このとき、毎年100円ずつ5年間もらうために、今どれだけ貯金しておけばよいかを資本回収係数を使って計算します。

計算の方法

まず、資本回収係数を求めるために、以下の式を使います

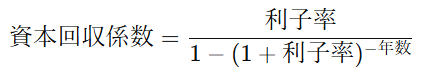
利子率が5%（0.05）、期間が5年間の場合、計算は次のようになります

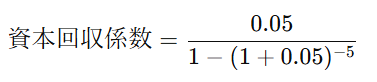
計算をすると

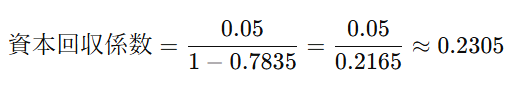
具体例

毎年100円ずつ5年間もらうためには、今どれだけ貯金しておけばいいかを計算します

つまり、毎年100円ずつ5年間もらうためには、今23.05円を貯金しておけばよいということです。

資本回収係数のまとめ

資本回収係数は、将来にわたって毎年一定の金額をもらうために、今どれくらいのお金を投資すればいいかを示す数字です。たとえば、将来毎年100円ずつ5年間もらいたいなら、今23.05円を貯金しておけばよいということです。この係数を使うことで、将来の定期的なお金を得るために必要な今の投資額を簡単に計算できます。